As I wrote from a train, when discussing Karatsuba multiplication: this academic year, I co-taught a module in Algorithms & Data Structures, given to our second-year undergraduates studying Computer Science or Games Programming. The syllabus covered a range of classic algorithms ranging from simple recursive numerical or linked-list computations, through searching and sorting, to string matching, dynamic programming and graph traversal, with some extra non-examinable stuff on the side; data structures included standard linear structures, hash tables, and a general discussion of suffix trees.
I put in a lot of effort in making coursework for the students. Ten
multiple-choice quizzes, each with about ten questions, each question
needing a hundred variants or so to prevent too much cheating; six
automatically-marked lab assignments, small implementations of
algorithms or data structures (each with unit tests written in both
Java and C++, because of course the two different degree programmes
use two different teaching languages); two peer-assessment exercises,
two independent essays (each on one of nine distinct topics, again to
prevent too much “sharing”...). Most of the coursework was
automatically graded – the students answered an average of 350
multiple-choice questions over the 10 weeks – but even so there were
200 two-page essays to grade and give feedback on, as well as guidance
for the peer assessments: and the need to write quiz questions often
kept me up on Sunday evenings well beyond the point of
sanityalertness.
However, all of that is now over and the results are in. (If you’re one of my students reading this between the time of writing and the time you receive your results: sorry!). One question might be: was all that effort worth it?
I don’t really believe that it’s possible to measure the effectiveness of teaching through student satisfaction scores or surveys. Indeed, as is often pointed out (e.g. Burke, Crozier and Misiasze, chapter 1), the process of learning is inherently uncomfortable, involving as it does a period of uncertainty and doubt: and students can’t necessarily judge how well they themselves have learnt. So looking at numerical scores from module evaluation surveys is pretty much doomed to meaninglessness, and even reading written feedback in detail needs to disentangle entertainment by a lecturer from learning facilitated by a lecturer.
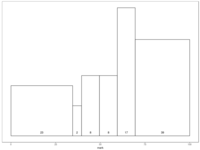
But it’s also not really possible to measure the effectiveness directly through marks. I can’t look at the marks students have achieved in the coursework I set: their marks are directly related to the pre-published marking schemes and assignment weightings, which will influence the students’ allocation of effort: and also, since I wrote the marking schemes and came up with the weightings, there’s a clear conflict in using the results as a judgment on whether the students have in fact learnt anything. Nevertheless, for the sake of completeness, here’s how the cohort did in their courseworks:
R> d <- read.csv("/tmp/is52038b.csv", na.strings=c("ABS", "NS"))
R> ggplot(d) + \
geom_histogram(aes(x=Final, y=..density..), color="black", fill="white", breaks=c(0, 34.5, 39.5, 49.5, 59.5, 69.5, 100)) + \
theme_bw() + \
theme(panel.grid.major=element_blank(), panel.grid.minor=element_blank()) + \
xlab("mark") + \
theme(axis.title.y=element_blank(), axis.ticks.y=element_blank(), axis.text.y=element_blank()) + \
stat_bin(aes(x=Final, y=..density..*0, label=..count..), breaks=c(0,34.5,39.5,49.5,59.5,69.5,100), geom="text", vjust=-1, size=2)
However, coursework should ideally have a formative effect. (Quality practitioners may wish to divide all assessments into separate “formative” and “summative” categories, but I believe that, with our students, having many notionally “summative” assignments with small mark allocations to strongly encourage students to actually do them is highly likely to help students with their major assessments: in other words, performing the function of formative assessment.) But formative for what?
Well, there’s an exam. And conveniently enough, my co-lecturer and I wrote the exam (and its marking scheme) before the students engaged in the coursework activities I described above. (They had done a perhaps more traditional workshop- and paper exercise-based coursework in the first term.) So we could examine whether there is any correlation between the mark achieved in the courseworks, using that as some kind of measure of engagement with the activities in question, and the final exam...
R> summary(lm(Exam~cwk1+cwk2, data=d))
Call:
lm(formula = Exam ~ cwk1 + cwk2, data = d)
Residuals:
Min 1Q Median 3Q Max
-33.465 -10.065 0.169 10.333 40.334
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 20.67228 6.64182 3.112 0.00252 **
cwk1 -0.04572 0.08655 -0.528 0.59870
cwk2 0.43467 0.07275 5.975 5.06e-08 ***
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
Residual standard error: 14.3 on 86 degrees of freedom
(10 observations deleted due to missingness)
Multiple R-squared: 0.3088, Adjusted R-squared: 0.2928
F-statistic: 19.21 on 2 and 86 DF, p-value: 1.264e-07
This simple regression, ostensibly showing a strong link between coursework 2 performance and exam performance, is far from conclusive. There are many factors involved in a student’s performance in assessment; students know their (provisional) coursework marks before they sit the exam, and might therefore choose to prioritise other activities if they are effectively guaranteed a passing grade anyway – and in any case it’s not clear what the ideal correlation between coursework and exam assessment might be: it’s probably larger than zero, on the basis that there is probably some element of aptitude or student engagement that remains constant – but it’s also probably smaller than one, because with perfect correlation what would be the point in separate assessments?
Nevertheless, I’m pretty pleased with how it all turned out, and I’ll be repeating and extending the approach, with an even larger number of small assessments with immediate feedback, in the next academic year.
(As well as lecturers, Goldsmiths Computing is currently recruiting a Reader and a post-doctoral researcher in Data Science. If you think I’m being awfully naïve by modelling marks, bounded between 0 and 100, with an unbounded error function, tell me about it and join in the fun!)